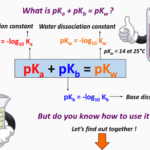
pH = -log10[H+], what is it, where to use it?
![ph = -log[h+] in Chemistry](https://topblogtenz.com/wp-content/uploads/2023/08/ph-logh-in-Chemistry-min.png)
The formula pH = -log[H+] unveils the relationship between the hydrogen ion concentration and the Universal scale used to measure the acidity or alkalinity of a chemical solution, i.e., the pH scale.
In this article, you will learn what are the components of pH = -log [H+] and how to use it for solving numerical questions.
However, before that, let us dive deep and find what is pH.
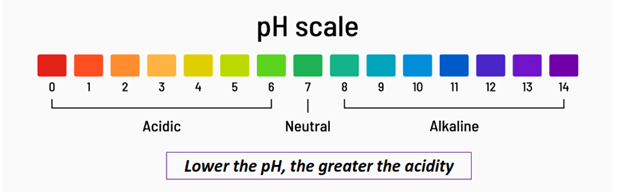
What is pH?
pH stands for the power of hydrogen.
The acidity or basicity of an aqueous solution is measured on a scale of 0 to 14, known as the pH scale.
Acidic solutions have a pH below 7, while basic solutions have a pH above 7. A pH exactly equal to 7 represents a neutral solution.
The greater the acidity of a solution, the lower its pH, and vice versa.
In contrast, the greater the basicity of an aqueous solution, the higher its pH value.
What is hydrogen ion concentration [H+]?
As per the Arrhenius concept, acidic substances release hydrogen ions (H+) in water.
Therefore, the greater the hydrogen ion concentration [H+] of an aqueous solution, the greater its acidity and vice versa.
This implies that there is a direct proportional relationship between the acidity of a solution and its hydrogen ion concentration.
Contrarily, the pH of the solution is inversely related to its acidity.
The formula pH = -log10 [H+] relates the pH of the solution to its hydrogen ion concentration.
What are the components of pH = -log[H+]?
The pH value of an aqueous solution can be determined by taking the negative logarithm of hydrogen ion concentration to the base 10.
Mathematically represented as pH = -log10[H+] where;
- pH = power of hydrogen. It is a numerical value from 0 to 14. (No units)
- [H+] = hydrogen ion concentration in the aqueous solution (Units = mol/L or M)
Where and how to use pH = -log [H+]? – Examples
If the concentration of hydrogen ions [H+] present in an aqueous solution is given, we can use it to find the pH by applying the formula:
![pH = -log [H+] formula in chemistry](https://topblogtenz.com/wp-content/uploads/2023/08/pH-log-H-formula-in-chemistry.png)
Pro-tip: Use your scientific calculator to solve such numerical problems.
In case the pH of a solution is given, we can find its hydrogen ion concentration [H+] by taking the antilog of pH as shown below:
[H+] = 10-pH
For example, The hydrogen ion concentration of an HCl solution is 0.050 mol/L. Find the pH of the aqueous solution by applying pH = -log [H+].
Solution
As per the question statement;
[H+] = 0.050 mol/L
pH = ?
So we can apply the formula pH = -log10 [H+] to find its pH as follows:
⇒ pH = -log10 [H+]
Substitute the value of [H+]:
pH = -log10 (0.050)
∴ pH = 1.30
Result: The pH of the 0.050 mol/L HCl solution is 1.30.
Another example is– Find the pH of a monoprotic acidic solution if the concentration of hydrogen ions in it is 4.5 x 10-3 mol/L.
As per the question statement;
[H+] = 4.5 x 10-3 mol/L
pH = ?
So we can apply the formula pH = -log10[H+] to find its pH as follows:
⇒ pH = -log10[H+]
Substitute the value of [H+]:
pH = -log10 (4.5 x 10-3)
∴ pH = 2.35
Result: The pH of the monoprotic acidic solution in this example is 2.35.
More examples on pH = -log[H+]
Calculate the concentration of hydrogen ions in moles per liter if the pH of the solution is 4.75. |
As per the question statement; pH = 4.75 [H+] = ? In this example, the value of pH is given while [H+] is unknown so we need to take the antilog of pH. ⇒ pH = -log10[H+] ∴ [H+] = 10-pH Substitute the value of pH: [H+] = 10-4.75 ∴ [H+] = 1.78 x 10-5 mol/L Result: The hydrogen ion concentration of the given solution is 1.78 x 10-5 mol/L. |
Calculate the pH of a 0.1 M solution of sulfuric acid (H2SO4) using pH = -log [H+]. |
The twist in this question is that sulfuric acid (H2SO4) is a diprotic acid, which means 2 moles of H+ ions are released per mole of H2SO4. This means [H+] = 2 [H2SO4] [H+] = 2 (0.1) = 0.2 M Now we can substitute [H+] into the formula: ⇒ pH = -log10 [H+] pH = -log10 (0.2) ∴ pH= 0.699 Result: The pH of 0.1 M H2SO4 solution is 0.699. |
FAQ
What does the formula pH = -log[H+] represent? |
In the formula pH = -log[H+]; pH = power of hydrogen. A numerical value from 0 to 14. [H+] = hydrogen ion concentration in mol/L or M. |
Which of the following options represents the correct pH formula?
|
Option D is the correct answer. pH is calculated by taking the negative logarithm to the base 10 of hydrogen ion concentration [H+], mathematically represented as pH = – log10 [H+]. |
How can we find hydrogen ion concentration [H+] if the pH of a monoprotic acidic solution is given? |
We can find [H+] by taking the antilog of pH as shown below: pH = – log10 [H+] [H+] = 10-pH |
As per pH = -log[H+], the pH of a solution containing a hydrogen ion concentration of 0.001 M is:
|
Option C is the correct answer. As per the question statement, hydrogen ion concentration = [H+]= 0.001 M Substituting the value of [H+] into the pH formula gives us: pH = – log10 [H+] pH = -log (0.001) ∴ pH = 3 Thus, the pH of the solution in this question is 3. |
About the author
Ammara Waheed is a highly qualified and experienced chemist, whose passion for Chemistry is evident in her writing. With a Bachelor of Science (Hons.) and Master of Philosophy (M. Phil) in Physical and Analytical Chemistry from Government College University (GCU) Lahore, Pakistan, with a hands-on laboratory experience in the Pakistan Council of Scientific and Industrial Research (PCSIR), Ammara has a solid educational foundation in her field. She comes from a distinguished research background and she documents her research endeavors for reputable journals such as Wiley and Elsevier. Her deep knowledge and expertise in the field of Chemistry make her a trusted and reliable authority in her profession. Let's connect - https://www.researchgate.net/profile/Ammara-Waheed
Related Posts: