Integration by parts for Definite integral problems with limits or bounds
Integration by parts for definite integral with limits, UV formulas, and rules
In this article, you will learn how to evaluate the definite integral using integration by parts UV formula. Generally, most of the students are confused about how to use the limit of the integral function after applying the integration by parts UV formula.

Integration by parts formula for solving definite integral limits problems-
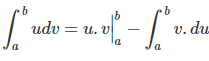
Rules for solving integration by parts for definite integral limits
1. The first one is that you can apply limits after the end of your integrating result as you did in indefinite integration but make sure your variable is the same.
Let’s take an example of \int _ { a } ^ { b } f ( y ) dx
⇒ First, solve the integration of this function
\int _ { a } ^ { b } f ( y ) dx = F ( y ) + C
⇒ then you put a limit in F(y)
\int _ { a } ^ { b } f ( y ) dx = F ( b ) – F ( a ) + C
2. The second one is that you can use the limit as you are going with integrals of functions. I recommended to you to use the second method when two or more functions are given as it minimizes your chance of error in Definite integral problems.
\int _ { a } ^ { b } udv = u.v \Big| _ a ^ b – \int _ { a } ^ { b } v.du
3. If you are using the first method then make sure first you solve integration as you do in indefinite integration then put the limit at the end of your result.
4. In the case of substitution integration, limits will keep changing depending on the substitution value.
So, you understand the rules and formulas of integration by parts for definite integral problems. If not, then we will understand it better by solving its examples. Let’s go-
Examples of Integration by parts for Definite integral limits/ Changing limits/ infinite limits
Example 1: Evaluate Definite Integral limits using integration by parts with both Rule 1 and 2.\int _ { 1 } ^ { 2 } x.lnx dx |
|
Solution: For solving the above definite integral problem with integration by parts using Rule 1, we have to apply limits after the end of our result First solve it, according to this: \int _ { } ^ { } u.dv = u.v – \int _ { } ^ { } v.du So, we have u = lnx and v = \frac { x ^ { 2 } } { 2 } [ ∴ dv = x ] ⇒ \int _ { } ^ { } lnx.xdx = lnx . \frac { x ^ { 2 } } { 2 } – \int _ { } ^ { } \frac { x ^ { 2 } } { 2 } . \frac { 1 } { x } = \int _ { } ^ { } lnx.xdx = lnx . \frac { x ^ { 2 } } { 2 } – \frac { x ^ { 2 } } { 4 } Now apply limits to evaluate definite integral ⇒ \int _ { 1 } ^ { 2 } lnx.xdx = \left [ lnx . \frac { x ^ { 2 } } { 2 } – \frac { x ^ { 2 } }{ 4 } \right ] \Big| _ 1 ^ 2 = \left [ ln2.2 – 1 \right ] – \left [ ln1. \frac { 1 } { 2 } – \frac { 1 } { 4 } \right ] [ ∴ \int _ { a } ^ { b } f ( y ) dx = F ( b ) – F ( a ) + C ] = ln4 – 1 + \frac { 1 } { 4 } = ln4 – \frac { 3 } { 4 } + C Answer Rule 2: The second rule said that you can use the limit as you are going with integrals of functions to solve integration by parts Definite integral with limits or bounds. According to this ⇒ \int _ { a } ^ { b } udv = u.v \Big| _ a ^ b – \int _ { a } ^ { b } v.du So, we have u = lnx and v = \frac { x ^ { 2 } } { 2 } [ ∴ dv = x ] ⇒ \int _ { 1 } ^ { 2 } lnx.x dx = lnx. \frac { x ^ { 2 } } { 2 } \Big| _ 1 ^ 2 – \int _ { 1 } ^ { 2 } \frac { x ^ { 2 } } { 2 } . \frac { 1 } { x } = \left [ 2ln2 – \frac { 1ln1 } { 2 } \right ] – \frac { 1 } { 2 } \int _ { 1 } ^ { 2 } x ^ { 2 } dx = \left [ ln4 – 0 \right ] – \left [ \frac { x ^ { 2 } } { 4 } \right ] \Big| _ 1 ^ 2 [ ∴ \int _ { a } ^ { b } f(y)dx = F ( b ) – F ( a ) + C ] = \left [ ln4 – 0 \right ] – \left [ 1 – \frac { 1 } { 4 } \right ] = ln4 – \frac { 3 } { 4 } + C Answer |
Example 2: Evaluate the definite integral using integration by parts with limits Rule 1
\int _ { 0 } ^ { \sqrt { 3 } } t ^ { 3 } ( 1 + t ^ { 2 } ) ^ { – 3 } dt
Solution:
Rule 1: First solve it by integration by parts as indefinite integral then use the limits
So we have integration by parts uv formula
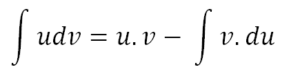
After solving this we get-
\int _ { } ^ { } t ^ { 3 } ( 1 + t ^ { 2 } ) ^ { -3 } dt = – \frac { 1 } { 4 } t ^ { 2 } ( 1 + t ^ { 2 } ) ^ { -2 } – \frac { 1 } { 4 } ( 1 + t ^ { 2 } ) ^ { -1 } + C
Now solve this using definite integral limits–
⇒ \int _ { 0 } ^ { \sqrt { 3 } } t ^ { 3 } ( 1 + t ^ { 2 } ) ^ { -3 } dt = \left [ – \frac { 1 } { 4 } t ^ { 2 } ( 1 + t ^ { 2 } ) ^ { – 2 } – \frac { 1 } { 4 } ( 1 + t ^ { 2 } ) ^ { – 1 } \right ] \Big| _ 0 ^ 3
= \left [ – \frac { 1 } { 4 } ( \sqrt { 3 } ) ^ { 2 } ( 1+ ( \sqrt { 3 } ) ^ { 2 } ) ^ { -2 } – \frac { 1 } { 4 } ( 1 + ( \sqrt { 3 } ) ^ { 2 } ) ^ { -1 } \right ] – \left [ – \frac { 1 } { 4 } ( 0 ) ^ { 2 } ( 1+ ( 0 ) ^ { 2 } ) ^ { – 2 } – \frac { 1 } { 4 } ( 1 + ( 0 ) ^ { 2 } ) ^ { -1 } \right ]
= – \frac { 3 } { 64 } – \frac { 1 } { 16 } + \frac { 1 } { 4 }
= \frac { 9 } { 64 } Answer
Example 3: Evaluate definite integral by Rule 2 of integration by parts\int _ { 0 } ^ { 2 } ( x + 1 ) e ^ { 4x } dx |
|
Solution: Rule 2: The second rule said you can use the limit as you are going with integrals of functions to solve integration by parts with limits or bounds. So we have, u = x + 1 dv = e4x According to this ⇒ \int _ { a } ^ { b } udv = u.v \Big| _ a ^ b – \int _ { a } ^ { b } v.du = \left [ ( x + 1 ) \frac { e ^ { 4x } } { 4 } \right ] \Big| _ 0 ^ 2 – \int _ { 0 } ^ { 2 } \frac { e ^ { 4x } } { 4 } dx = \left [ ( 2 + 1 ) \frac { e ^ { 8 } } { 4 } – \frac { 1 } { 4 } \right ] – \left [ \frac { e ^ { 4x } } { 16 } \right ] \Big| _ 0 ^ 2 = \left [ ( 2 + 1 ) \frac { e ^ { 8 } } { 4 } – \frac { 1 } { 4 } \right ] – \left [ \frac { e ^ { 8 } } { 16 } – \frac { 1 } { 16 } \right ] = \frac { 11 } { 16 } e ^ { 8 } – \frac { 3 } { 16 } Answer |
Example 4: Evaluate definite integral with an infinite limit by integration by parts second rule\int _ { 0 } ^ { \infty } x.e ^ { -x } dx |
|
Solution: Rule 2: \int _ { a } ^ { b } udv = u.v \Big| _ a ^ b – \int _ { a } ^ { b } v.du Let u = x and dv = e-x ⇒ \int _ { 0 } ^ { \infty } x.e ^ { -x } dx = \left [ -xe ^ { -x } \right ] \Big| _ 0 ^ \infty + \int _ { 0 } ^ { \infty } -e ^ { -x } dx (∴ v = -e-x ) = \left [ -xe ^ { -x } \right ] \Big| _ 0 ^ \infty + \left [ -e ^ { -x } \right ] \Big| _ 0 ^ \infty = \left [ -xe ^ { -x } -e ^ { -x } \right ] \Big| _ 0 ^ \infty Take limit extent to infinity = \lim _ { x \rightarrow \infty } \left [ -xe ^ { -x } -e ^ { -x } \right ] – \left [ -0.e ^ { -0 } – e ^ { -0 } \right ] = \left [ 0 -0 \right ] – \left [ 0 – 1 \right ] = 1 Answer |
Example 5: Evaluate Definite integral by changing limit of integration by parts using Rule 2\int _ { 0 } ^ { 1 } t \sqrt { t + 2 } dt |
|
Solution: According to the Rule 2 ⇒ \int _ { a } ^ { b } udv = u.v \Big|_a ^ b – \int _ { a } ^ { b } v.du Let u = t and dv = \sqrt { t + 2 } dt v = \frac { 2 } { 3 } ( t + 2 ) ^ { 3/2 } Now put value in integration by part with limit formula = \frac { 2 } { 3 } t( t + 2 ) ^ { 3/2 } \Big|_ 0 ^ 1 – \int _ { 0 } ^ { 1 } \frac { 2 } { 3 } ( t + 2 ) ^ { 3/2 } dt = \frac { 2 } { 3 } t ( t + 2 ) ^ { 3/2 } \Big| _ 0 ^ 1 – [ \frac { 4 } { 15 } ( t + 2 ) ^ { 5/2 } ] \Big| _ 0 ^ 1 = \frac { 2 } { 3 } ( 3 ) ^ { 3/2 } – \frac { 4 } { 15 } ( 3 ^ { 5/2 } – 2 ^ { 5/2 } ) Answer |
Hope you understand that how can we solve the integration by parts for Definite integrals with limits or bounds problems, its substitution rules, formulas, etc.
Also check –
About the author
Vishal Goyal is the founder of Topblogtenz, a comprehensive resource for students seeking guidance and support in their chemistry studies. He holds a degree in B.Tech (Chemical Engineering) and has four years of experience as a chemistry tutor. The team at Topblogtenz includes experts like experienced researchers, professors, and educators, with the goal of making complex subjects like chemistry accessible and understandable for all. A passion for sharing knowledge and a love for chemistry and science drives the team behind the website. Let's connect through LinkedIn: https://www.linkedin.com/in/vishal-goyal-2926a122b/
