Estimating ph without calculator

Short for the ‘power of hydrogen’’ pH is a numerical measure of the acidity or alkalinity of a chemical solution. From the tang of a freshly squeezed lemon to the bitter texture of soaps and detergents, pH plays an important role.
What is pH?
pH determines the hydrogen ion concentration [H+] of an aqueous solution. It ranges from a numerical value of 0-14 on the pH scale.
Acids have a pH below 7 while bases have a pH above 7. A pH exactly equal to 7 represents a neutral solution.

The greater the acidity of an aqueous solution, the lower its pH value, and vice versa for basicity.
How to estimate the pH of a chemical solution?
The rough estimation of pH can be done by performing conventional tests such as using a litmus paper or a Universal pH indicator paper.
The litmus paper is a simple indicator of pH. It only tells whether a chemical solution is acidic or basic in nature.
When dipped into an aqueous solution, it changes color from purple to red if the solution is acidic (pH < 7) or blue in the presence of a basic solution (pH > 7).
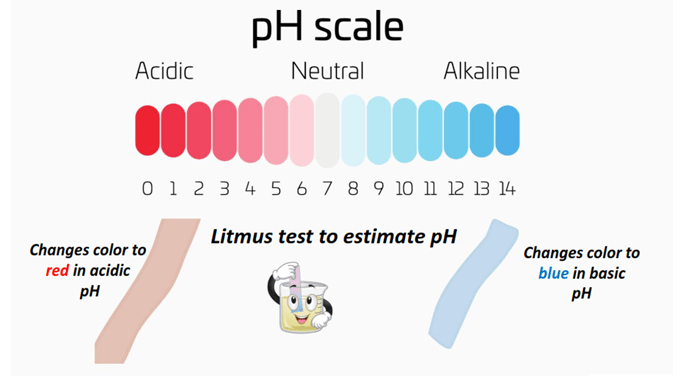
The Universal pH indicator paper provides a better pH approximation as compared to the litmus paper.
When dipped into the aqueous solution, the color obtained can be matched against the colors given on the pH scale to estimate the pH of the solution within a broader range.
However, a narrow pH estimation requires applying the pH formula without performing any physical tests.
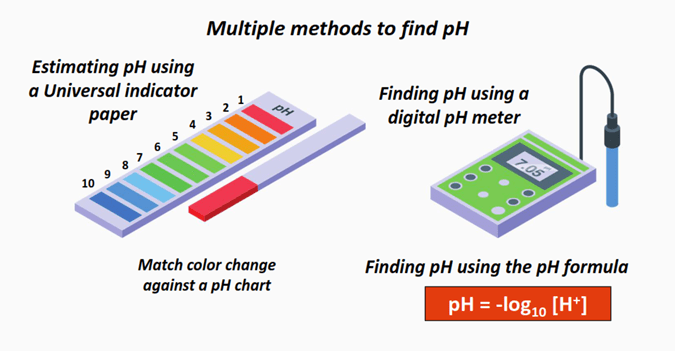
What is the formula to calculate pH?
The formula to calculate pH is:
pH = -log10 [H+]……Equation (I)
Where [H+] = Molar concentration of hydrogen ions (Units: mol/L or mol/dm3) while pH is a unitless entity.
But how to use the above formula to find pH if a calculator is not allowed? Well in this article, we will teach you exactly that i.e., some tried and tested tips and tricks to estimate pH without a calculator.
How to use pH = -log10 [H+] to estimate pH without a calculator?
We can find the approximate value of the negative log of a quantity by using the short trick given below.
-log (m x 10-n) = n – 0.m
For example, if the hydrogen ion concentration [H+] of a given aqueous solution is 2 x 10-3 mol/L, then we can find its pH as follows:
⇒ pH = -log10 [H+]
pH = -log10 (2 x 10-3)
Here m = 2 and n = 3 so the approximate pH value is:
∴ pH = 3 – 0.2 = 2.8
The actual value of –log10 (2 x 10-3) = 2.70. As you can see, the value determined above (2.8) is quite close to 2.70, hence assured we can conveniently use the above trick to estimate the pH value for a solution whose hydrogen ion concentration is known.
Now let’s try another example.
Another example is- Find the pH of a monoprotic acidic solution if the concentration of hydrogen ions in it is 4.5 x 10-3 mol/L, without using a calculator.
Solution:
As per the question statement,
[H+] = 4.5 x 10-3 mol/L
pH = ?
Applying the pH formula:
⇒ pH = -log10 [H+]
Substituting the known value of [H+]:
pH = -log10 (4.5 x 10-3)
Applying the approximation trick:
⇒ pH = -log (m x 10-n) = n – 0.m
Here m = 4.5 = 5 and n = 3
pH = 3 – 0.5
∴ pH = 2.5
Result: The approximate pH of the given solution is 2.5.
Furthermore, you can learn from the table given below some common log values and use these to estimate the pH of a solution as follows:

We know from our previous example that [H+] = 4.5 x 10-3 mol/L. Applying the pH formula:
pH = -log10 (4.5 x 10-3)
As per the general log principles (log ab = log a + log b), the above formula can be split as follows:
pH = -[log10 4.5 + log10 10-3]
4.5 = 5 and log10 ab = b log10 a
pH = – [log10 5 + (-3 log10 10)]
Substituting the log values from the above table gives us:
pH = – [ 0.70 + (-3 (1)]
pH = – 0.70 + 3
∴ pH = 2.3
The answer obtained via this method (2.3) is even closer to the actual pH value [-log10 (4.5 x 10-3) = 2.35] as compared to what we obtained previously (2.5), hence ensuring this method of pH estimation is more accurate.
What if the pH of a solution is given and we need to find its [H+]? Let’s explore this in the next section.
How to find [H+] or [H3O+] without a calculator?
Equation (I) can be rearranged as follows:
[H+] = 10-pH…..Equation (II)
Thus, the hydrogen ion or hydronium ion concentration of an aqueous solution can be determined by taking the antilog of pH to the base 10.
However, the twist here is, doing that without a calculator.
Let’s see an example – Given that the pH of an aqueous solution is 3, find its hydrogen ion concentration [H+] in mol/L, without using a calculator.
Solution:
As per the question statement,
pH = 3
[H+] = ?
Applying the formula,
⇒ [H+] = 10-pH
Substituting the known value of pH:
[H+] = 10-3
10-3 is easy to calculate as shown below.
∴ [H+] = 1/1000 = 0.001
Result: The hydrogen ion concentration of the given solution is 0.001 mol/L.
Now, lets see an example of finding [H+] without a calculator when pH is not an integer.
Let’s see an example – Given that the pH of an aqueous solution is 5.67, find its hydrogen ion concentration [H+] in mol/L, without using a calculator.
Solution:
As per the question statement,
pH = 5.67
[H+] = ?
Applying the formula,
⇒ [H+] = 10-pH
Substituting the known value of pH:
[H+] = 10-5.67
5.67 = 5 + 0.67 so the above expression can be rewritten as follows:
[H+] = 10-(5 +0.67)
As per the mathematical principles of the log,
5 = log10 105 (Proof: log10 105 = 5 log10 10 = 5(1) = 5)
0.67 = 0.7, and the log table tells us that log 2 = 0.7 so substituting log10 2 in place of 0.67 and log10 105 in place of 5 in the above formula, meanwhile replacing 10– with the word antilog for simplicity gives us:
[H+] = Antilog (log10 105 + log10 2)
⇒ log a + log b = log ab
∴ [H+] = Antilog (log10 (105 x 2))
Antilog (10-x) is canceled with log, finally giving us the required hydrogen ion concentration:
∴ [H+] = 2 x 105 = 0.000002
Result: The estimated hydrogen ion concentration of the given solution is 0.000002 mol/L which is quite close to the actual value i.e., 0.00000214.
How to find pOH without a calculator?
pOH is calculated by taking the negative logarithm to the base 10 of the hydroxide ion concentration [OH–] of an aqueous solution.
pOH = -log10 [OH–]…..Equation (III)
So, you can easily find the pOH of an aqueous solution, given its [OH–] using the log rules discussed previously.
For example, Find the pOH of an aqueous solution, without using a calculator, given that its hydroxide ion concentration is 0.003 mol/L.
Solution:
As per the question statement,
[OH–] = 0.003 mol/L
pOH = ?
Applying the formula,
⇒ pOH = -log10 [OH–]
Substituting the known value of [OH–]:
pOH = -log10 (0.003)
0.003 = 3 x 10-3 so the above formula can be rearranged as:
pOH = -log10 (3 x 10-3)
Applying the log principles and substituting the values from the general log table gives us:
pOH = – (log10 3 + log10 10-3)
pOH = -[log10 3 + (-3 log10 10)]
pOH = -[0.48 – 3(1)]
∴ pOH = -0.48 + 3 = 2.52
Result: The pOH of the given solution is 2.52.
pOH is related to pH by the formula given below:
pH + pOH = 14…..Equation (IV)
This means we can also find the pOH of a chemical solution, given its pH, [H+] or [H3O+].
Let’s see an example- Find the pOH of a solution given that its [H3O+] = 4.5 x 10-5 mol/L.
Solution:
As per the question statement,
[H3O+] = 4.5 x 10-5 mol/L
pOH = ?
An acid dissociates in water as follows:
HA + H2O → H3O+ + A–
[H3O+] = [H+] given that the concentration of water [H2O] stays constant.
∴ pH = -log10 [H+] = -log10 [H3O+]
Substituting the known value:
pH = -log10 (4.5 x 10-5)
pH = -[log10 4.5 + log10 10-5]
pH = -[log10 4.5 – 5 log10 10]
As 4.5 lies midway between 4 and 5 so we can estimate that log 4.5 = [(log 4) + (log 5)]/2.
Substituting the log values from the general table gives us = [(0.60 + 0.70)/2] = 0.65.
∴ pH = – [log10 4.5 – 5 log10 10] = – 0.65 + 5(1) = 4.35
Now that we know the pH of the solution, we can comfortably find its pOH as follows:
⇒ pH + pOH = 14
∴ pOH = 14 – pH = 14 – 4.35 = 9.65
Result: The estimated pOH of the given solution is 9.65.
How to find Ka and pKa without a calculator?
Ka is another parameter for measuring the strength of an acid. It stands for the acid dissociation constant.
The greater the strength of an acid, the higher its Ka value while it possesses a lower pKa.
For the reversible dissociation of a weak acid:
HA (aq) + H2O (l) ⇌ H3O+ (aq) + A–(aq)
Ka = [H+][A–]/[HA]
pKa is calculated by taking the negative logarithm of Ka:
pKa = -log10 Ka…..Equation (V)
Let’s practice an example: 0.20 mol/L acetic acid dissociates in water such that the equilibrium concentration of hydrogen ions is 0.05 mol/L. Find Ka and pKa without using a calculator.
Solution:
Acetic acid dissociates in water as follows:
CH3COOH (aq) ⇌ CH3COO–(aq) + H+ (aq)
The Ka expression for the above equation is:
Ka = [H+][CH3COO–]/[CH3COOH]
As per the balanced chemical equation, 1 mole of acetic acid (CH3COOH) dissociates to produce 1 mole of each of acetate (CH3COO–) and hydrogen (H+) ions.
[CH3COO–] eq = [H+] eq = 0.05 mol/L
[CH3COOH] eq = 0.20 – 0.05 = 0.15 mol/L
Substituting the above data into the Ka expression and doing some manual calculations gives us:
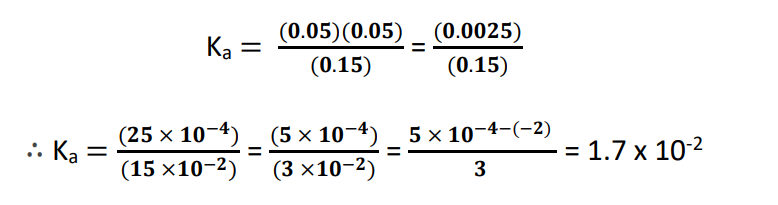
Now finding pKa:
pKa = -log10 (1.7 x 10-2)
pKa = -[log10 1.7 +(-2 log10 10)]
Approximating, 1.7 = 2
pKa = – [log10 2 – 2 log10 10]
∴ pKa = – 0.30 + 2(1) = 1.7
Result: The Ka value is 1.7 x 10-2 while the estimated pKa of the given acetic acid solution is 1.7.
FAQ
How to estimate the pH of a given solution without a calculator? |
We can estimate the pH of a chemical solution by performing some physical tests i.e. using a litmus paper or a Universal pH indicator. The color change gives an estimation of the pH of the solution. In contrast, if its hydrogen ion concentration [H+] is given, we can find its pH numerically by applying the formula: pH = -log10 [H+] Substituting the given value of [H+] and applying general log principles, the required pH can be easily determined. |
How can we find [OH–] if the pH of a solution is given? |
To find [OH–] from pH, we can follow the two simple steps given below:
|
What is the relation between the Ka of an acidic substance with the pH of its aqueous solution? |
Ka of an acidic substance is inversely related to the pH of its aqueous solution. The higher the Ka value, the more strongly it dissociates in an aqueous solution to liberate a large number of H+ ions, thus it possesses a low pH value as pH is calculated by taking the negative log of hydrogen ion concentration to the base 10, pH = -log10 [H+]. |
About the author
Ammara Waheed is a highly qualified and experienced chemist, whose passion for Chemistry is evident in her writing. With a Bachelor of Science (Hons.) and Master of Philosophy (M. Phil) in Physical and Analytical Chemistry from Government College University (GCU) Lahore, Pakistan, with a hands-on laboratory experience in the Pakistan Council of Scientific and Industrial Research (PCSIR), Ammara has a solid educational foundation in her field. She comes from a distinguished research background and she documents her research endeavors for reputable journals such as Wiley and Elsevier. Her deep knowledge and expertise in the field of Chemistry make her a trusted and reliable authority in her profession. Let's connect - https://www.researchgate.net/profile/Ammara-Waheed